Category: entertainment

Harry Plotter: Shiny App of Spell Usage

In my second Harry Plotter blog (22-Aug-2017), I wrote:

I would like to demonstrate how regular expressions can be used to retrieve (sub)strings that follow a specific format. We could use regex to examine, for instance, when, and by whom, which magical spells are cast.

Well, Prusinowskik (real name unknown) beat me to it, and how! S/He formed a comprehensive list of all spells found in the Harry Potter saga (see below), and categorized these into “spells“, “charms“, and “curses“, and into “popular“, “dueling” and “unforgivable” purposes. Next, Prusinowskik built an interactive Shiny application with lovely JavaScript graphs (package: rCharts) for us to discover precisely when during the saga which spells are cast (see also below). Moreover, the analysis was repeated for both the books and the movies.

Truly excellent work Prusinowskik! The Shiny app can be found here.

spells_dash — Overview of dueling spells (interactive)

The House Always Wins: Simulating 5,000,000 Games of Baccarat a.k.a. Punto Banco

The associated GitHub repository with R code.

Past weekend, I visited the casino with some friends. Of all games, we enjoy North-American-style Baccarat the most. This type of Baccarat is often called Punto Banco. In short, Punto Banco is a card game in which two hands compete: the “player” and the “banker“. During each coup (a round of play), both hands get dealt either 2 or 3 cards, depending on a complex drawing schema, and all cards have a certain value. Put simply, the hand with the highest total value of cards wins the coup, after which a new one starts. Before each coup, gamblers may bet which of the hands will win. Neither hand is in any way associated with the actual house or player/gambler, so bets may be placed on both. All in all, three different bets can be placed in a game of Punto Banco:

The player hand has the highest total value, in which case the player wins (Punto);
The banker hand has the highest total value, in which case the banker wins (Banco);
The player and banker hands have equal total value, in which case there is a tie (Egalité).

If a gambler correctly bets either Punto or Banco, their bets get a 100% payoff. However, a house tax will often be applied to Banco wins. For instance, Banco wins may only pay off 95% or specific Banco wins (e.g., total card value of 5) may pay off less (e.g., 50%). Depending on house rules, a correct bet on a tie (Egalité) will pay off either 800% or 900%. A wrong bet on Punto or Banco stands in case Egalité is dealt. In all other cases of wrong bets, the house takes the money.

My friends and I like Punto Banco because it is completely random but seems “gameable”. Punto Banco is played with six or eight decks so there is no way to know which cards will be next. Moreover, the card-drawing rules are quite complex, so you never really know what’s going to happen. Sometimes both Punto and Banco get only two cards, at other times, the hand you bet on will get its third card, which might just turn things around. Punto Banco’s perceived gameability comes through our human fallacies to see patterns in randomness. Often, casino’s will place a monitor with the last fifty-so results (see below) to tempt gamblers to (erroneously) spot and bet on patterns. Alternatively, you might think it’s smart to bet against the table (play Punto when everybody else goes for Banco) or play on whatever bet won last hand. As the hands are dealt quite quickly in succession, and the minimal bet is often 10+ euro/dollar, Punto Banco is a quick way to find out how lucky you are.

Image result for punto banco scoreboard — Examples of Baccarat monitors, often placed next to a table.

So back to last weekend’s trip to the casino. Unfortunately, my friends and I lost quite some money at the Punto Banco table. We know the house has an edge (though smaller than in other games) but normally we are quite lucky. We often discuss what would be good strategies to minimize this houses’ edge. Obviously, you want to play as few games as possible, but that’s as far as we got in terms of strategy. Normally, we just test our luck and randomly bet Punto or Banco, and sparsely on Egalité.

As a statistical programmer, I thought it might be interesting to simulate the game and its odds from the bottom up. On the one hand, I wanted to get a sense of how favorable the odds are to the house. On the other hand, I was curious as to what extent strategies may be more or less successful in retaining at least some of your hard-earned cash.

In my simulations, I follow the Holland Casino Punto Banco rules, meaning a six-deck shoe and a Banco win with 5 pays out 50%. I did adopt the more lenient 9-1 payoff for Egalité though. Several hours of programming and some million simulated Baccarat hands later, here are the results:

Do not play Baccarat / Punto Banco if you do not want to lose your money. Obviously, it’s best to not set foot in the casino if you can’t afford to lose some money. However, I eagerly pay for the entertainment value I get from it.
You lose least if you stick to Banco. Despite having only a 50% payoff when Banco wins with 5, the odds are best for Banco due to the drawing rules. Indeed, according to the Wizard of Odds, the house edge for Banco (1.06%) is slightly lower than that of Punto (1.24%).
Whatever you do, do not bet on Egalité. Because most casino’s pay out 8 to 1 in case of a correctly predicted tie, betting on one seems about the worst gambling strategy out there. With a house edge of over 14%, you are better off playing most other games (Wizard of Odds). Although casino’s paying out a tie 9 to 1 decrease the house edge to just below 5%, this is still way worse than playing either Punto or Banco.

The figure below shows the results of the five strategies I tested using 50,000 simulations of 100 consecutive hands. Based on the results, I was reluctant to develop and test other strategies as results look quite straightforward: play Banco. Additionally, Wikipedia cites Thorp (1984, original reference unknown) who suggested that there are no strategies that will really result in any significant player advantage, except maybe for the endgame of a deck, which presumably requires a lot of card counting. If you nevertheless want to test other strategies, please be my guest, here are my five:

Punto: Always bet on Punto.
Banco: Always bet on Banco.
Egalité: Always bet on Egalité.
LastHand: Bet on the outcome of the last hand/coup.
LastHand_PB: Bet on the outcome of the last hand/coup, only if this was Punto or Banco.

The above figure depicts the expected value of each strategy over a series of consecutive hands played. Clearly, the payoff is quite linear, independent of your strategy. The more hands you play, the more you lose. However, also clear is that some strategies outperform others. After 100 hands of Baccarat, playing only Banco will on average result in a total loss below the amount you wager. For example, if you bet 10 euro every hand, you will have a loss of about 9 euro’s after 100 rounds, on average. This is in line with the ~1% house edge reported by the Wizard of Odds. Similarly, betting only Punto will result in a loss of about 130% of the bet amount, which is also conform the ~1.4% house edge reported by the Wizard of Odds. Betting on Punto or Banco based on whichever won last (LastHand_PB) performs somewhere in between these two strategies, losing just over 100% of the bet amount in 100 hands. Your expected losses increase when you just bet on whichever outcome came last, including Egalité, resulting in around ~-150% after 100 hands. This is mainly because betting on Egalité, which seems about the worst strategy ever, will result in a remarkable 493.9% loss after 100 hands.

Apart from these average or expected values, I was also interested in the spread of outcomes of our thousands of simulations. Particularly because gamblers on a lucky streak may win much more when betting on Egalité, as the payoff is larger (8-1 or 9-1). The figure below shows that any strategy including Egalité will indeed result in a wider spread of outcomes. Betting on Egalité may thus be a good strategy if you are by some miracle divinely lucky, have information on which cards are coming next, or have an agreement with the dealer (disclaimer: this is a joke, please do not ever bet on Egalité with the intention of making money or try to cheat at the casino).

If you want to know how I programmed these simulations, please visit the associated github repository or reach out. I intend on simulating the payoff for various other casino games in the near future (first up: BlackJack), so if you are interested keep an eye on my website or twitter.

Join 385 other subscribers

Animated Snow in R

Due to the recent updates to the gganimate package, the code below no longer produces the desired animation.
A working, updated version can be found here.

After hearing R play the Jingle Bells tune, I really got into the holiday vibe. It made me think of Ilya Kashnitsky (homepage, twitter) his snowy image in R.

– Papa, what are you doing?
…
How I ended up generating #rstats snow for my 3yo daughter Sophia#ggplot2 #dataviz pic.twitter.com/29sk1HpROJ
— Ilya Kashnitsky (@ikashnitsky) 4 december 2017

if(!"tidyverse" %in% installed.packages()) install.packages("tidyverse")

library("tidyverse")

n <- 100 
tibble(x = runif(n),  
y = runif(n),  
s = runif(n, min = 4, max = 20)) %>%
ggplot(aes(x, y, size = s)) +
geom_point(color = "white", pch = 42) +
scale_size_identity() +
coord_cartesian(c(0,1), c(0,1)) +
theme_void() +
theme(panel.background = element_rect("black"))

This greatly fits the Christmas theme we have going here. Inspired by Ilya’s script, I decided to make an animated snowy GIF! Sure R is able to make something like the lively visualizations Daniel Shiffman (Coding Train) usually makes in Processing/JavaScript? It seems so:

### ANIMATED SNOW === BY PAULVANDERLAKEN.COM
### PUT THIS FILE IN AN RPROJECT FOLDER

# load in packages
pkg <- c("here", "tidyverse", "gganimate", "animation")
sapply(pkg, function(x){
if (!x %in% installed.packages()){install.packages(x)}
library(x, character.only = TRUE)
})

# parameters
n <- 100 # number of flakes
times <- 100 # number of loops
xstart <- runif(n, max = 1) # random flake start x position
ystart <- runif(n, max = 1.1) # random flake start y position
size <- runif(n, min = 4, max = 20) # random flake size
xspeed <- seq(-0.02, 0.02, length.out = 100) # flake shift speeds to randomly pick from
yspeed <- runif(n, min = 0.005, max = 0.025) # random flake fall speed

# create storage vectors
xpos <- rep(NA, n * times)
ypos <- rep(NA, n * times)

# loop through simulations
for(i in seq(times)){
if(i == 1){
# initiate values
xpos[1:n] <- xstart
ypos[1:n] <- ystart
} else {
# specify datapoints to update
first_obs <- (n*i - n + 1)
last_obs <- (n*i)
# update x position
# random shift
xpos[first_obs:last_obs] <- xpos[(first_obs-n):(last_obs-n)] - sample(xspeed, n, TRUE)
# update y position
# lower by yspeed
ypos[first_obs:last_obs] <- ypos[(first_obs-n):(last_obs-n)] - yspeed
# reset if passed bottom screen
xpos <- ifelse(ypos < -0.1, runif(n), xpos) # restart at random x
ypos <- ifelse(ypos < -0.1, 1.1, ypos) # restart just above top
}
}

# store in dataframe
data_fluid <- cbind.data.frame(x = xpos,
y = ypos,
s = size,
t = rep(1:times, each = n))

# create animation
snow <- data_fluid %>%
ggplot(aes(x, y, size = s, frame = t)) +
geom_point(color = "white", pch = 42) +
scale_size_identity() +
coord_cartesian(c(0, 1), c(0, 1)) +
theme_void() +
theme(panel.background = element_rect("black"))

# save animation
gganimate(snow, filename = here("snow.gif"), title_frame = FALSE, interval = .1)

Updates:

21/12/2017: Keith combined sound and image to create this very merry video.
22/12/2017: Ioannis Kosmidis generated snow in base R
25/12/2017: Daniel Shiffman dedicated a coding challenge to the topic.
25/12/2017: Cynthia Siew combined sound and image in this Shiny Christmas card.
17/12/2018: Due to the update to gganimate, I updated the code and general setup to run still in 2018.

Jingle Bells in R

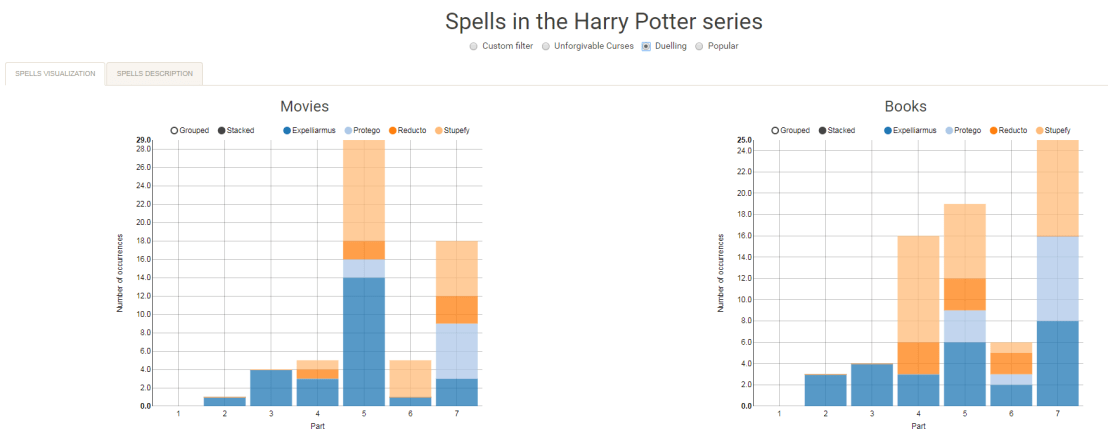
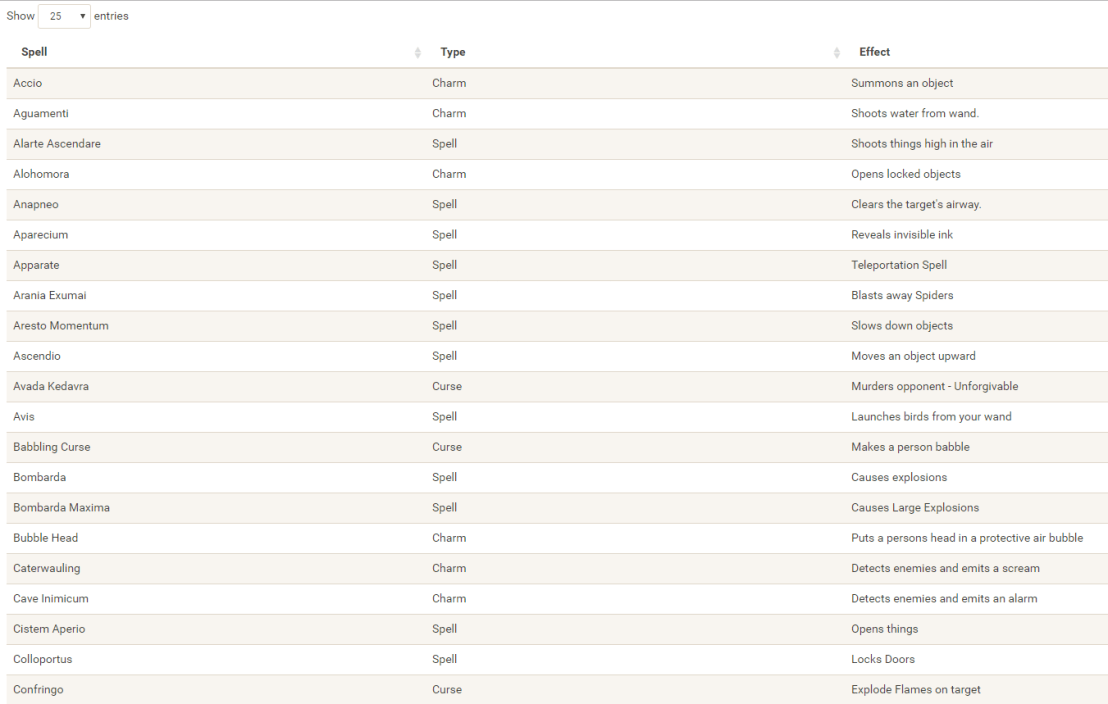
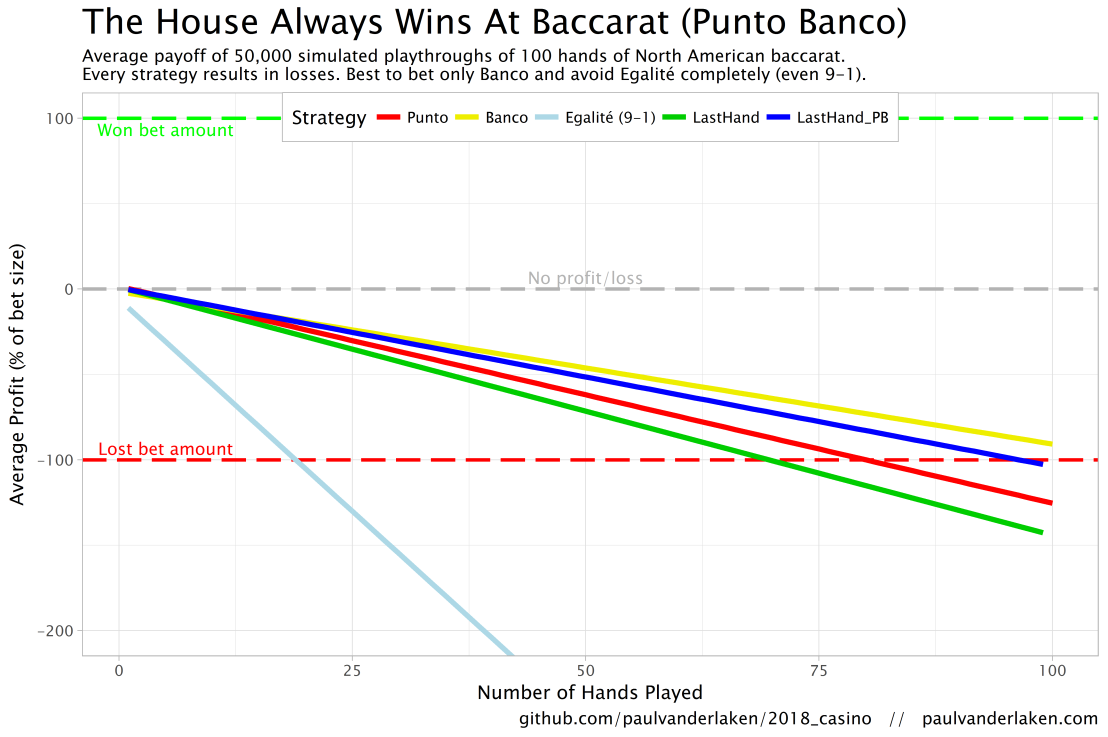
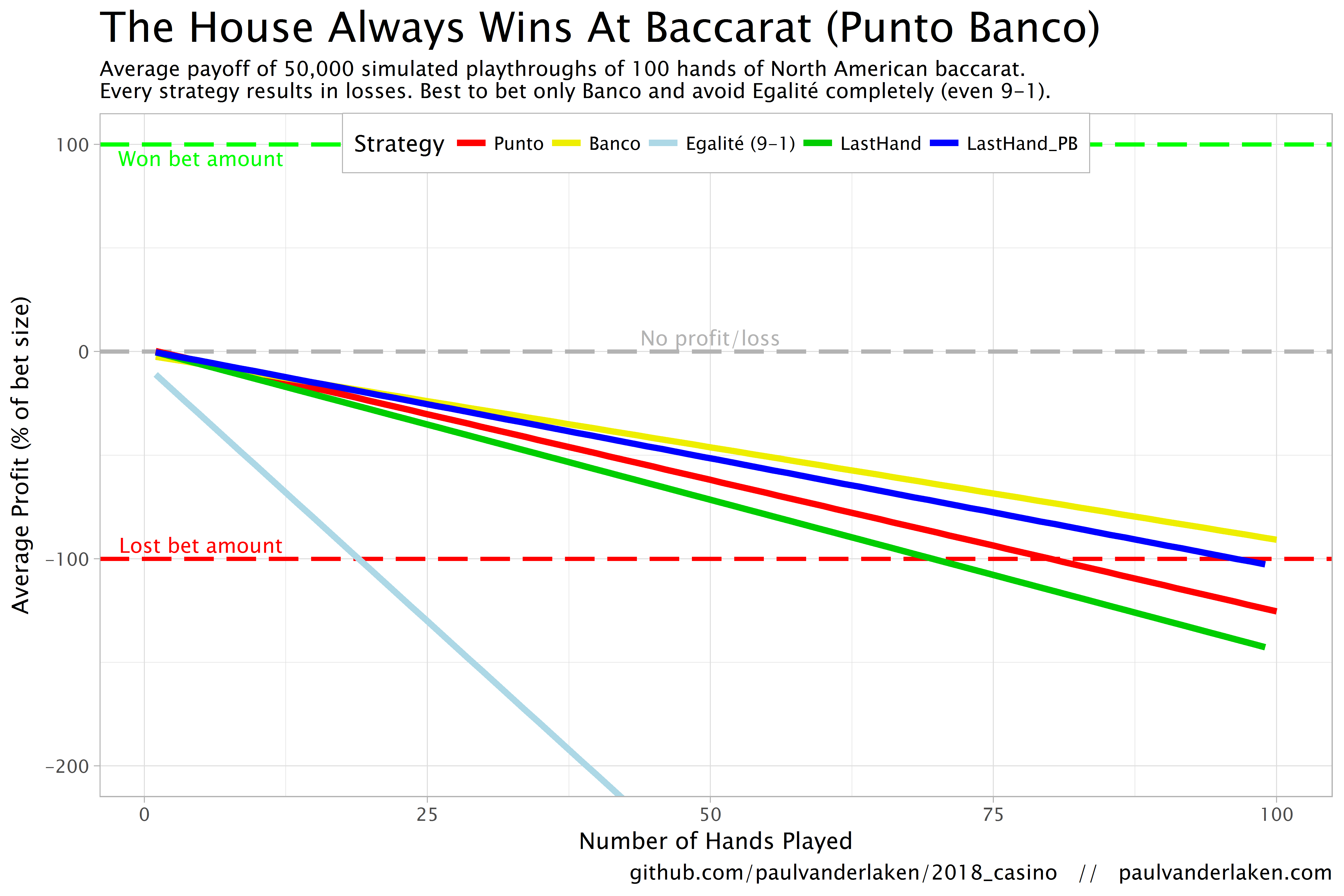
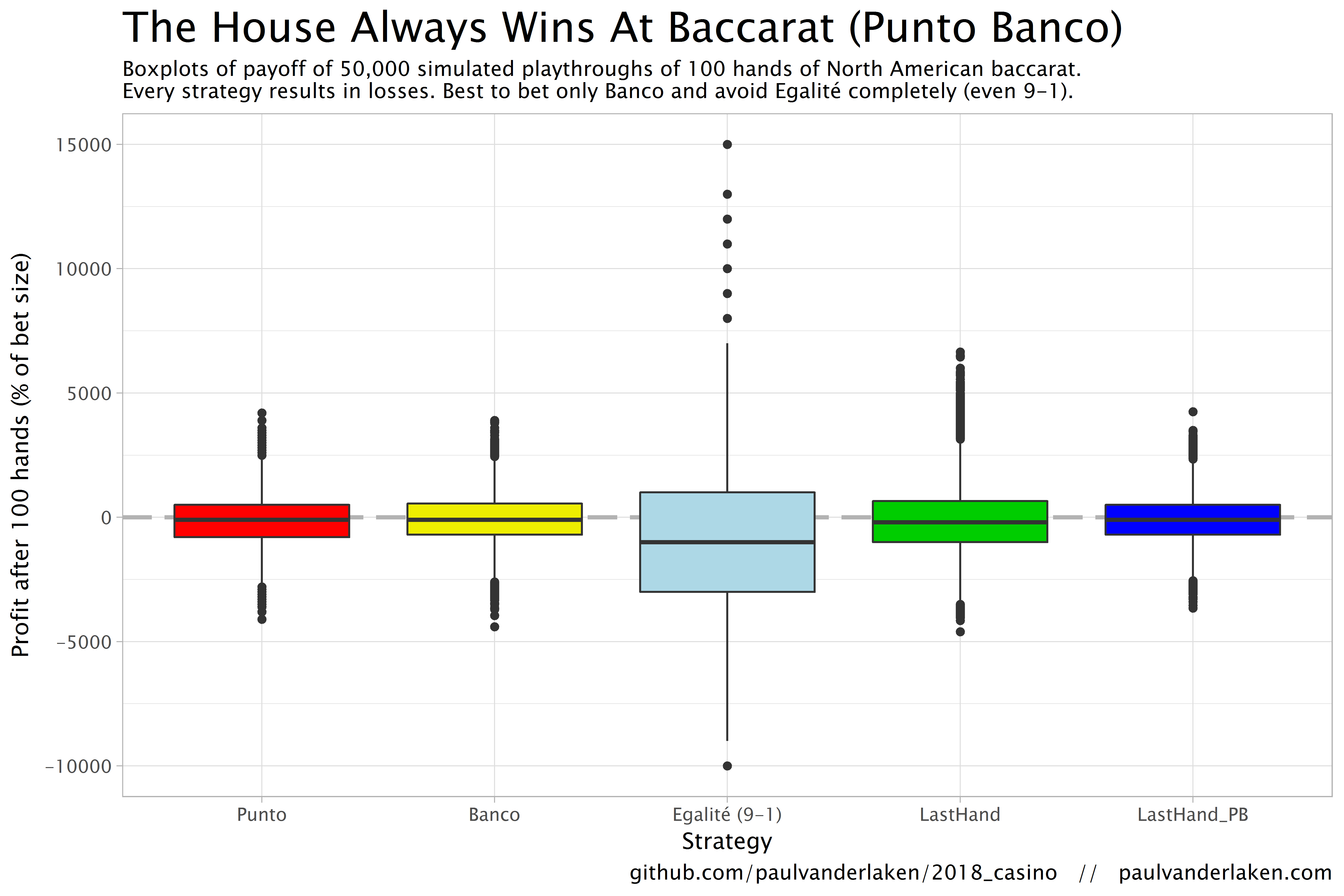
Christmas is here! Keith McNulty called on his LinkedIn network to co-create a script to play Christmas tunes. After adding some notes myself, the R script on this github page now plays Jingle Bells. The final tune you can download here and the script I pasted below. Any volunteers to make Let it snow or Silent night?

2018/12/19: Keith combined the full Jingle Bells script and my snow animation into a video.
2108/12/20: Mark Burkey posted R Jingle Bells on YouTube as well as a versions of Silent Night (R script) and Let It Snow (Rscript).

if(!"dplyr" %in% installed.packages()) install.packages("dplyr")
if(!"audio" %in% installed.packages()) install.packages("audio")

library("dplyr")
library("audio")

notes <- c(A = 0, B = 2, C = 3, D = 5, E = 7, F = 8, G = 10)

pitch <- paste("E E E",
"E E E",
"E G C D",
"E",
"F F F F",
"F E E E",
"E D D E",
"D G",
"E E E",
"E E E",
"E G C D",
"E",
"F F F F",
"F E E E E",
"G G F D",
"C",
"G3 E D C",
"G3",
"G3 G3 G3 E D C",
"A3",
"A3 F E D",
"B3",
"G G F D",
"E",
"G3 E D C",
"G3",
"G3 E D C",
"A3 A3",
"A3 F E D",
"G G G G A G F D",
"C C5 B A G F G",
"E E E G C D",
"E E E G C D",
"E F G A C E D F",
"E C D E F G A G",
"F F F F F F",
"F E E E E E",
"E D D D D E",
"D D E F G F E D",
"E E E G C D",
"E E E G C D",
"E F G A C E D F",
"E C D E F G A G",
"F F F F F F",
"F E E E E E",
"G C5 B A G F E D",
"C C E G C5")

duration <- c(1, 1, 2,
1, 1, 2,
1, 1, 1.5, 0.5,
4,
1, 1, 1, 1,
1, 1, 1, 1,
1, 1, 1, 1,
2, 2,
1, 1, 2,
1, 1, 2,
1, 1, 1.5, 0.5,
4,
1, 1, 1, 1,
1, 1, 1, 0.5, 0.5,
1, 1, 1, 1,
4,
1, 1, 1, 1,
3, .5, .5,
1, 1, 1, 1,
4,
1, 1, 1, 1,
4,
1, 1, 1, 1,
4,
1, 1, 1, 1,
4,
1, 1, 1, 1,
3, 1,
1, 1, 1, 1,
1, 1, 1, 1,
1, 1, 1, 1,
1, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,
1, 1, 0.5, 0.5, 0.5, 0.5,
1, 1, 0.5, 0.5, 0.5, 0.5,
0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,
0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,
1, 0.5, 0.5, 1, 0.5, 0.5,
1, 0.5, 0.5, 1, 0.5, 0.5,
1, 0.5, 0.5, 0.5, 0.5, 1,
1, 0.33, 0.33, 0.33, 1, 0.33, 0.33, 0.33,
1, 1, 0.5, 0.5, 0.5, 0.5,
1, 1, 0.5, 0.5, 0.5, 0.5,
0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,
0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,
1, 0.5, 0.5, 1, 0.5, 0.5,
1, 0.5, 0.5, 1, 0.5, 0.5,
0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,
1, 0.33, 0.33, 0.33, 2)

jbells <- data_frame(pitch = strsplit(pitch, " ")[[1]],
duration = duration)

jbells <- jbells %>%
mutate(octave = substring(pitch, nchar(pitch)) %>%
{suppressWarnings(as.numeric(.))} %>%
ifelse(is.na(.), 4, .),
note = notes[substr(pitch, 1, 1)],
note = note + grepl("#", pitch) -
grepl("b", pitch) + octave * 12 +
12 * (note < 3),
freq = 2 ^ ((note - 60) / 12) * 440)

tempo <- 250

sample_rate <- 44100

make_sine <- function(freq, duration) {
wave <- sin(seq(0, duration / tempo * 60, 1 / sample_rate) *
freq * 2 * pi)
fade <- seq(0, 1, 50 / sample_rate)
wave * c(fade, rep(1, length(wave) - 2 * length(fade)), rev(fade))
}

jbells_wave <- mapply(make_sine, jbells$freq, jbells$duration) %>%
do.call("c", .)

play(jbells_wave)

So You Think You Can (A/B) Test?

Decision making under uncertainty is complicated. These days, many business rely on real-life experiments, or A/B tests, to reduce that uncertainty and improve their decision-making. For instance, here’s a presentation on how A/B testing helps improve business outcomes at Etsy.

Lukas Vermeer built So You Think You Can Test, an online simulation game in which you are the decision-maker in a company. You control the backlog and running of experiments and each day you have to decide which tasks to prioritize (or deleted entirely). Your decisions affect the sales of the company, so be wise and use the experimental information to your advantage.

You can play the game here.

Facial Recognition Challenge: Chad Smith & Will Ferrell

The below summarizes Part 4 of a medium.com series by Adam Geitgey.
Check out the original articles: Part 1, Part 2, Part 3, Part 4, Part 5, Part 6, Part 7 and Part 8!

Adam Geitgey likes to write about computers and machine learning. He explains machine learning as “generic algorithms that can tell you something interesting about a set of data without you having to write any custom code specific to the problem. Instead of writing code, you feed data to the generic algorithm and it builds its own logic based on the data.” (Part 1)

*Adam’s visual explanation of two machine learning applications (original from Part 1)*

In the fourth part of his series on machine learning Adam touches on Facial Recognition. Facebook is one of the companies using such algorithms in real-time, allowing them to recognize your friends’ faces after you’ve tagged them only a few times. Facebook reports they recognize faces with 97% accuracy, which is comparable to our own, human facial recognition abilities!

Facebook’s algorithms recognizing and automatically tagging Adam’s family. Helpful or creepy? (original from Part 4)

Adam decided to put up a challenge: would a facial recognition algorithm be able to distinguish Will Ferrell (famous actor) from Chad Smith (famous rock musician)? Indeed, these two celebrities look very much alike:

Image result for will ferrell chad smith — Chad Smith (left) and Will Ferell (right) on www.rollingstone.com

If you want to train such an algorithm, Adam explain, you need to overcome a series of related problems:

First, look at a picture and find all the faces in it

Second, focus on each face and be able to understand that even if a face is turned in a weird direction or in bad lighting, it is still the same person.

Third, be able to pick out unique features of the face that you can use to tell it apart from other people— like how big the eyes are, how long the face is, etc.

Finally, compare the unique features of that face to all the people you already know to determine the person’s name.

(Adam Geitgey, Part 4)

How the facial recognition algorithm steps might work (original from Part 4)

To detect the faces, Adam used Histograms of Oriented Gradients (HOG). All input pictures were converted to black and white (because color is not needed) and then every single pixel in our image is examined, one at a time. Moreover, for every pixel, the algorithm examined the pixels directly surrounding it:

Illustration of the algorithm as it would take in a black and white photo of Will Ferrel (original from Part 4)

The algorithm then checks, for every pixel, in which direction the picture is getting darker and draws an arrow (a gradient) in that direction.

Illustration of how algorithm would reduce a black and white photo of Will Ferrel to gradients (original from Part 4)

However, to do this for every single pixel would require too much processing power, so Adam broke up pictures in 16 by 16 pixel squares. The result is a very simple representation that does capture the basic structure of the original face, based on which we can now spot faces in pictures. Moreover, because we used gradients, the result will be similar regardless of the lighting of the picture.

The original image turned into a HOG representation (original from Part 4)

Now that the computer can spot faces, we need to make sure that it knows that two perspectives of the same face represent the same person. Adam uses landmarks for this: 68 specific points that exist on every face. An algorithm can then be trained to find these points on any face:

The 68 points on the image of Will Ferrell (original from Part 4)

Now the computer knows where the chin, the mouth and the eyes are, the image can be scaled and rotated to center it as best as possible:

The image of Will Ferrell transformed (original from Part 4)

Adam trained a Deep Convolutional Neural Network to generate 128 measurements for each face that best distinguish it from faces of other people. This network needs to train for several hours, going through thousands and thousands of face pictures. If you want to try this step yourself, Adam explains how to run OpenFace’s lua script. This study at Google provides more details, but it basically looks like this:

The training process visualized (original from Part 4)

After hours of training, the neural net will output 128 numbers accurately representing the specific face put in. Now, all you need to do is check which face in your database is most closely resembled by those 128 numbers, and you have your match! Many algorithms can do this final check, and Adam trained a simple linear SVM classifier on twenty pictures of Chad Smith, Will Ferrel, and Jimmy Falon (the host of a talkshow they both visited).

In the end, Adam’s machine had learned to distinguish these three people – two of whom are nearly indistinguishable with the human eye – in real-time: